While playing Norman Wildberger’s second video lecture on the “fundamental group” I heard material I have never addressed before – despite it being 20 years after I got Cameron’s course for computer scientists on fields, rings, groups, etc. It’s just fascinating to see/hear the geometric angle. This would make a far better second year engineer-math component of a science degree than the typically awfully taught linear algebra course.
https://www.youtube.com/watch?v=E6f3I-RiWbk&feature=player_detailpage#t=1503
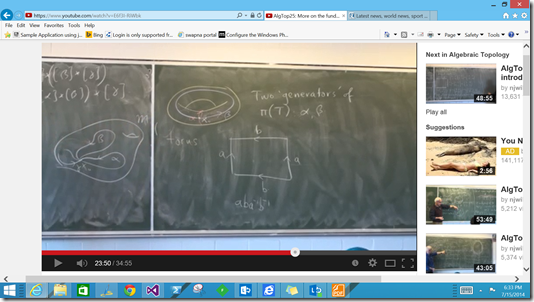
Its just fascinating to see Wildburger after touching on multiplication and inverses apply the technique to the abstract torus – where there are 2 dimensions/generators to the (constant) loop.
https://www.youtube.com/watch?v=E6f3I-RiWbk&feature=player_detailpage#t=1503
At this point we start to think more about Turing’s On Permutation’s model – having seen that Turing has simply added another geometry to those that Wildberger gives as examples.
https://www.youtube.com/watch?v=E6f3I-RiWbk&feature=player_detailpage#t=1503
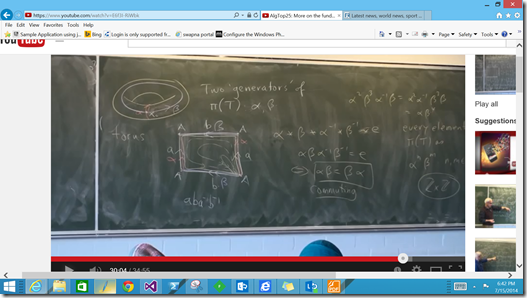
The theory gives us some quite “involved” modeling terms to work with commutativity, powers of path-functions, commutators and sets of generators on a particular surface (that constrains loops).
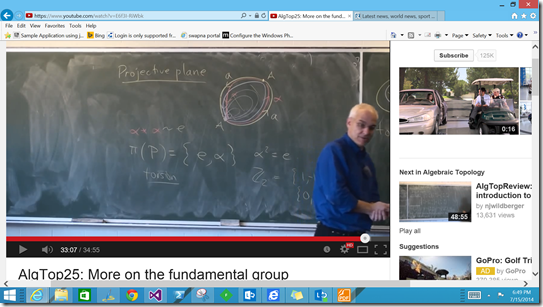
We even see something clearly modeled (algebraically by Turing) in the use of the projective plane as the base space for a covering domain argument. This addresses the special case in which powers of a generator can only equal the identity term.
https://www.youtube.com/watch?v=E6f3I-RiWbk&feature=player_detailpage#t=1503
The course element has given us several examples of “torshioning” (contraction).
We should remember, now, that Turing’s main point in his manuscript was that certain wiring plans for the Turing bombe drums produce a surface and a supporting algebra (and yes a unwanted bombe in 1950 would be allowing him to several wheels in series!). The U terms play the role of Alpha (to some power). Of course, the symbol of “U to some power” can be expanded as the U wheel being rotated foreward or backward by the power – as in setting an enigma box – such that alphabets of two wheels conjugate.
When a set of such rotated wheels have powers that sum to zero, we have the commuting “normal” case of course. When such powers sum to zero, we see also that we have the “definition” of the abstract cycle (vs a not-cycle that is)– as thought in the world of higher-dimensional homotopic spaces.