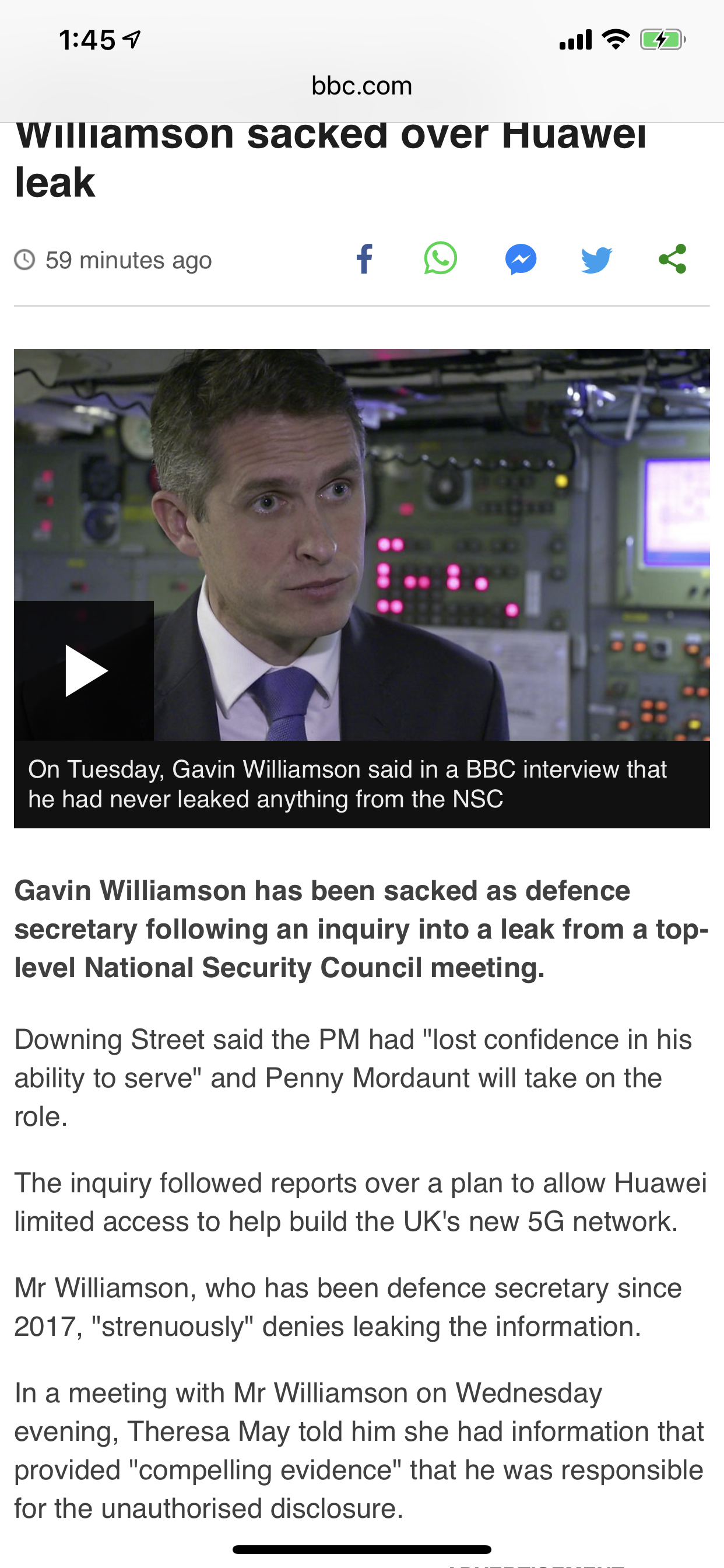
The MPK mini mkII is an ultra-compact keyboard controller designed for the traveling musician and the desktop producer. With an…
— Read on www.akaipro.com/kb/akai-pro-mpk-mini-mkii-complete-setup-in-pro-tools-first/
Akai Pro MPK mini mkII – Complete Setup in Pro Tools First | Akai Professional
Fox news and china align
Whats the beef bbc?

Analyze china if you wish.
But state how its different to cnn and foxnews presenting different spins…
Otherwise bbc/uk looks like a bolton-grade hack duping a former London mayor…
Sell Mexico/ solve the immigration issue?
Or sell the uk, now its actually for sale!
Like when cali got “purchased”, expect to be stripped of everything in exchange for crappy education, endless strip malls, lots of dollars (in boom/bust cycle) and really great healthcare (but only if you can afford it)

May and trumps ineptness
The leak could only come from the top, as a political payback gesture on the way out of the door.
Its also a good test to see where the Americans are spying on Britain.
Special relationship (in spying) or not, they cannot but spy! Its their nature!
Which tells you where to ultimately trust.
Id dump the ww2 5-eyes spying culture, given brexit. Replace it with a franco/german/british joint venture, that looks forward. not ec, but still euro.
No small size #condon now in abandoned us/uk trade deal
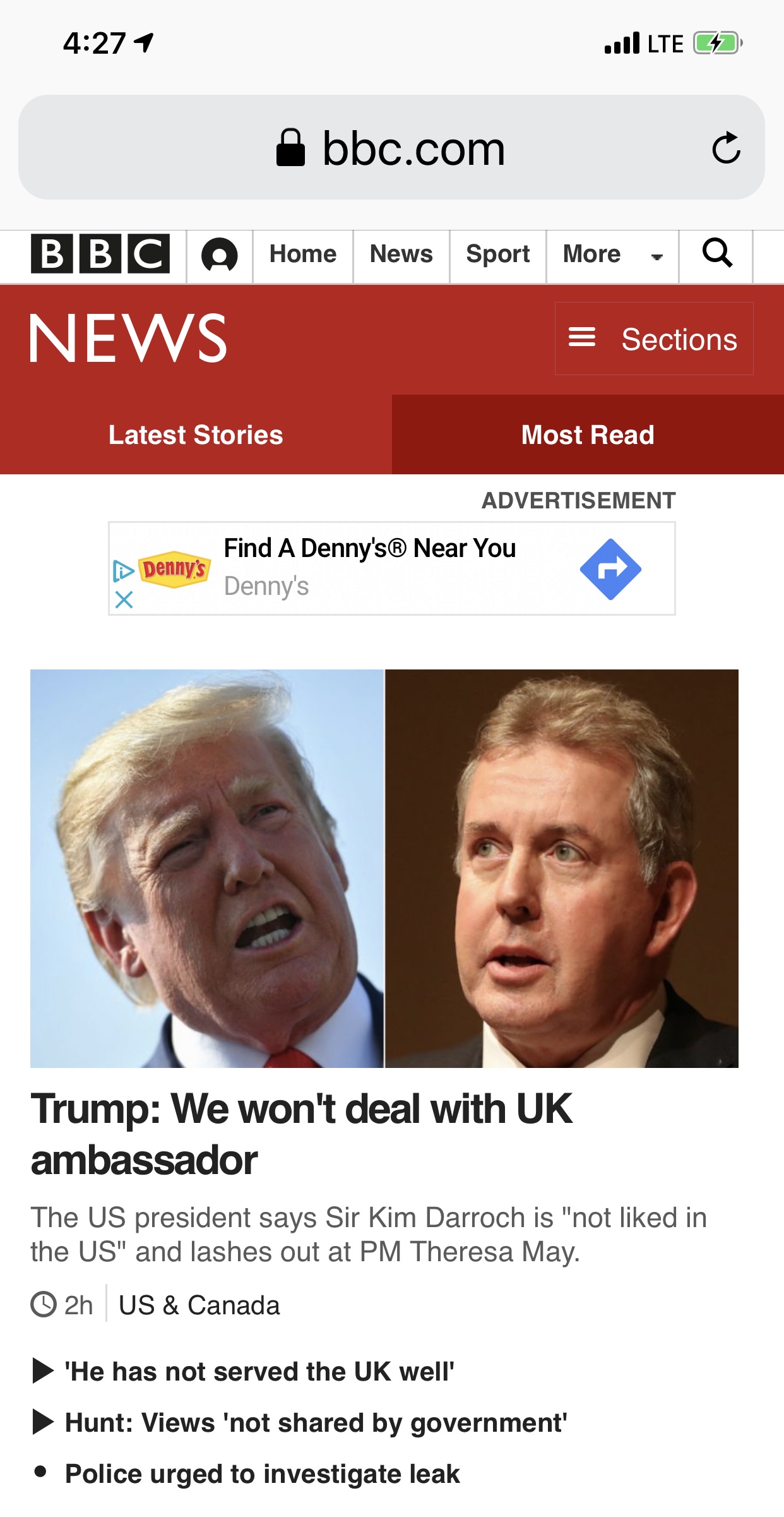
Thats torn it!
Cut off from eu (french) ones due to brexit, and now denied small trump-branded condons from the us, whats the uk going to do?
Easy. Choose a leader who was a boy student at eton…(sure to hire his old eton friends too).
Iranian cyber response
If its true that the usa just used em And related cyber against the computer and/controllers of “Iranian-made” missile batteries, there is an appropriate counter response – assuming it succeeded.
Its a savvy Islamic response.
Disclose in great detail how it works, what its impact was, how you go about fixing…your analysis of the how the supply chain was fixed ip (years ago) to either deliver unsuitable chip packages (or corrupt that batch, for your delivery)
Etc
The thing they will hate about all that is the disclosure of how and why (as now everyone with contaminated chips also goes and upgrades). You just “force multiplied…” using their internet against them.
Btw space-rad hardening requires certain orbit based experiments, to master the knowhow. Good use for those icbms…
Piano playing crank
Enigma/tunny decibans explained musically

See https://www.notreble.com/buzz/2010/02/18/math-and-music-equations-and-ratios/
So now we have the knowhow to add weights… when doing tunny/colossus code breaking.
Its just tuning in…
probability concepts explained_ maximum likelihood estimation
Is a good intro to the logic of the code break of runny.
For a more concise statement, see


From

Why do uk veterans respect trump (the dodger)
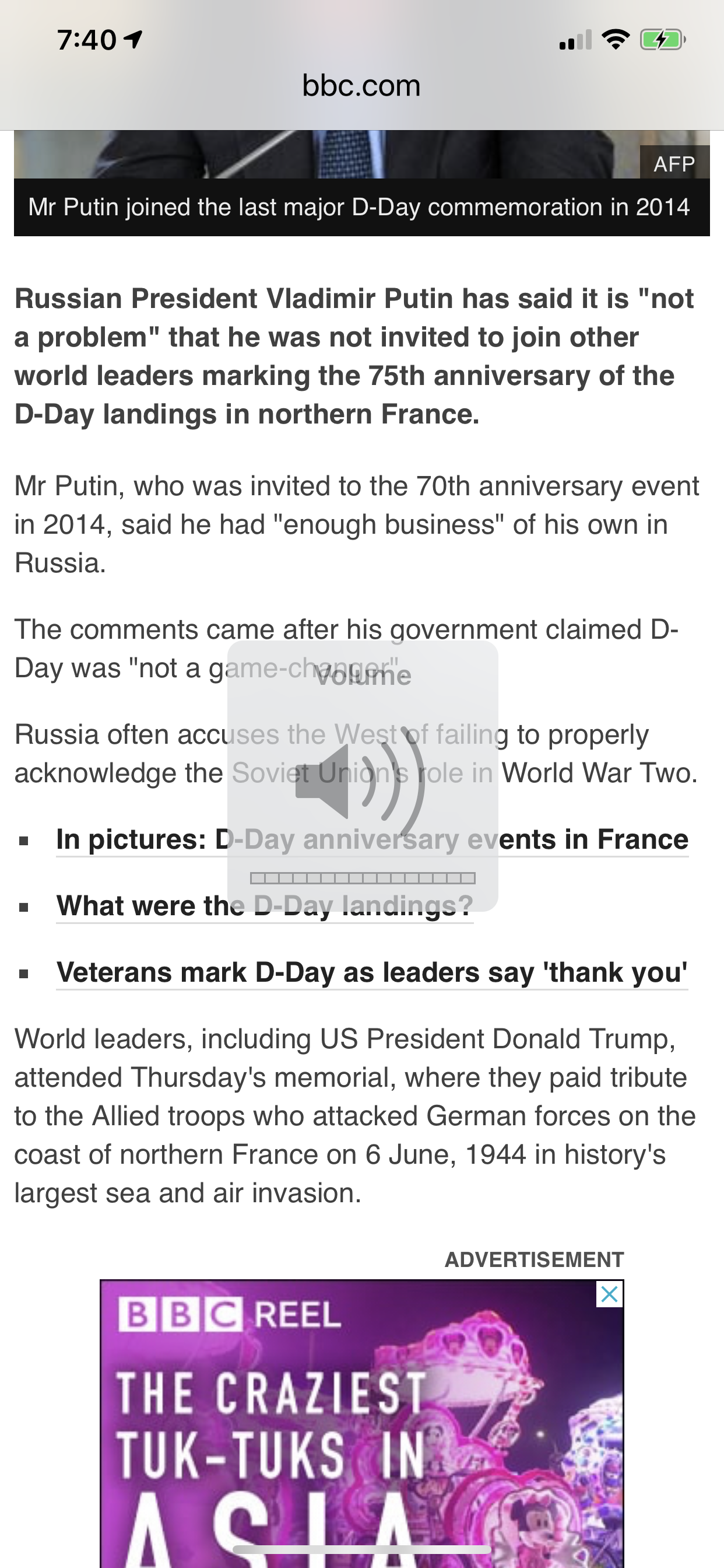
I get it.
You did a (n indoctrinated) duty. Uk , French, otherwise and (exceptional) American.
But trump didn’t (and neither did may). And neither did i.
Did many dead Russians make d/day easier (by far)? Yes.
Ive never met a hero who said otherwise.
Ive met a lot of fox news trumpista false heroes (mental age 13) though.
Light them up, they all said. Smirking the fox news smirk.
Respect.
Piano history book
China students: uk welcomes you
Same cost.
Welcoming people (in London anyways)
Easy to migrate us credits…
School quality sane or better…
France and Germany (Italy/ greece) right next door..

Teary-eyed American freedom (anthem blaring)
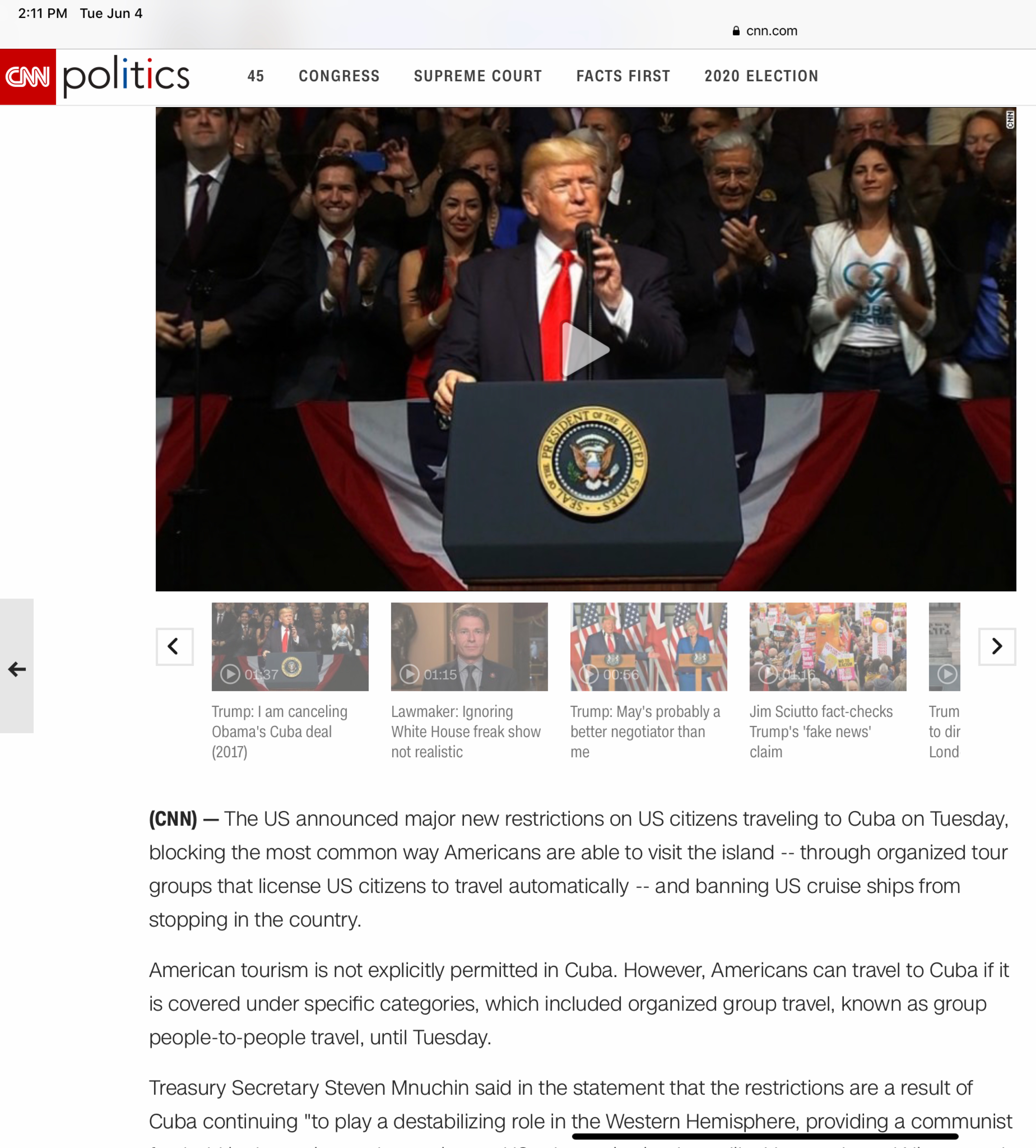
Seems American freedom is a bit limited.
Kinda like being born free (but enslaved a second later)
Wonderful!
Which are the britons?

Pretty obvious. The ones sidelined , irrelevant, ignored and huddled in a little group for mutual support.
Dupus, potus pottyus and free world democracy
Lets give farage his new title: dupus, endorsed in person by potus pottyus, the infamous (roman?) emperor of the free world, democratically elected by almost none of its members – in typical USA fashion – not that huge portions of the population have a vote. (Washington would be proud).
Melania us coverup
When her pointy heels go in the grass, what happened?
Coverup!

Ok mexicans. How long it take to get a generator up to the private fence and cut out a hole??
Dont hurt a public fence. But a private fence is fair game (since they can sue you easily).
Every day you cut, post a social media blog of its new fallibility (and drive ip the cost of “protecting the fence itself”).
Paint slogans in the us side… something rude and vulgar.
(Nothing will annoy them more… than constant demo of its ineffectiveness… and the perpetual recurring costs…
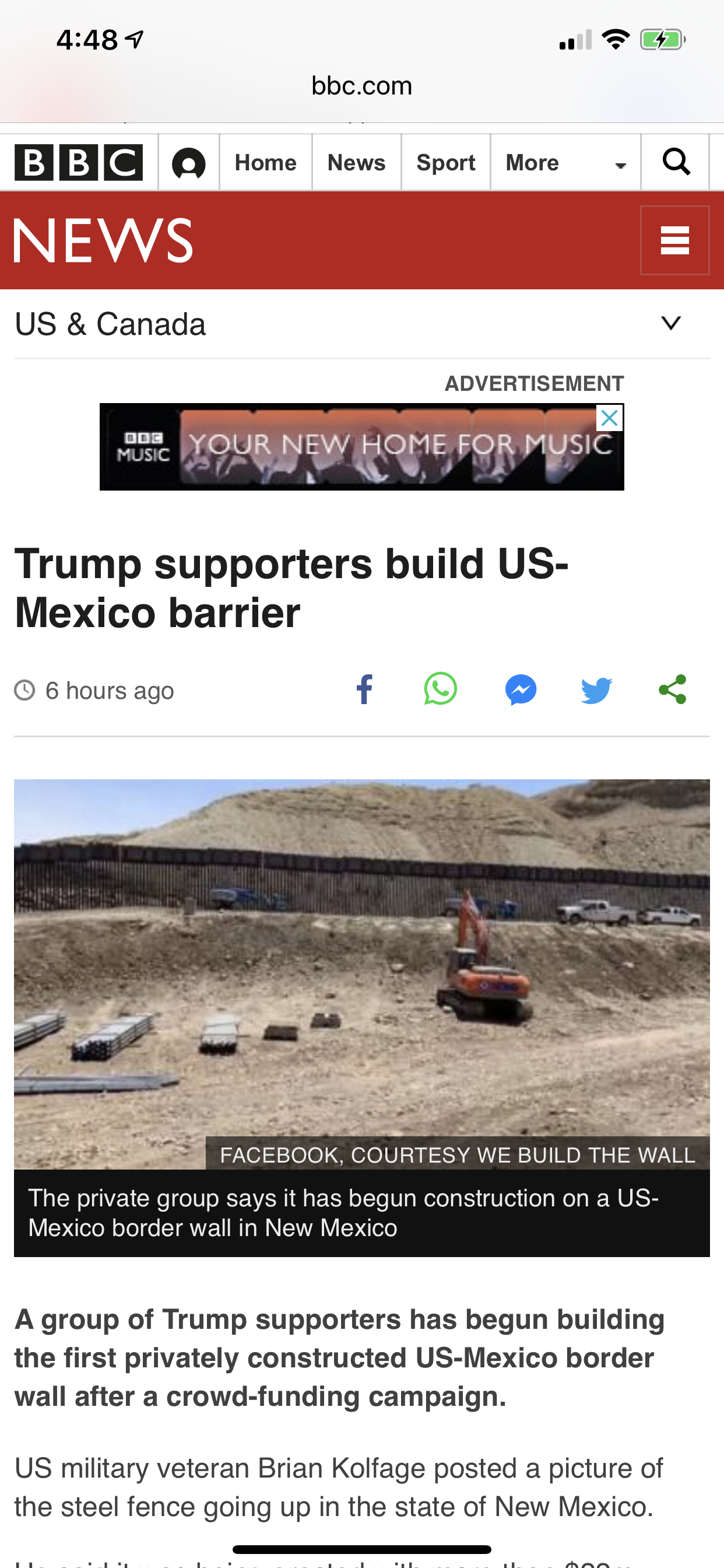
Taubman summarized
Such good news for post brexit uk (as the usa withdraws globally)

Every empire has its fall and decline: including that of the usa
As the old, imperially-motivated usa withdraws from markets (in fit of pique), the new uk gets to enter the vacated space with networking and bridge building skills – for a post usa (post-post british empire) world.
The trick is to now get off the American drug, recognizing the cost of addiction (when the dealer suddenly withdraws supply to pressure the demand curve) so one can be free again – to build what the uk is good at: a cooperative and just space, where no-one can dominate but all can constructively build without sone uniforms (eg yanqui exceptionalism) dogma.
Id you are sone old mi6 director worried about your us book deal and post govt consultancy fees, you probably disagree. Wonder why (missing out on your cut of the drug deal)?
,
Conman and danny torching tendencies
With king trump empowered to threaten his modern (not hewish) enemies with a good (danny-like) torching (the whole, full wrath of manic Moses pissed at being historically known as the first all American slaver) we can evaluate the got narratives ending.
Didn’t it end with the power woman dead, the pretty princess off happy in her castle, and the boys back to first order of business: rebuilding the brothels? …
…Presumably to be branded and frequented by king trump, loser of the kings moot!
China tariffing dethrone the trump empire
What Id do, as china, is release news of each retaliatory tariff category once a day, on each news day for a month
Neutralize the bit about greatness (to strut, to warn, and all the other imperious language games)
Make (news) america bored again of hearing about yet another retaliatory tariff category .
Affects trump personally, then.
Makes his imperious mannerisms look well old fashioned and imperious!
Iranian asymmetric nukes
In my latest dream i was strategizing for Persia, given Trump now has to “start and win a quick war” to get re-elected. My avatar saud ( woops said) , go nuclear – without the showy explosion (which is to unIsamic and all too full of yanqui hell hath no more fury than the inherently pissed off New England Puritans)
Powder the spend nuclear fuel (quick now, the avatar urged) and scrape a scratch in the metal casing of these gazzilion tiny short range rockets. Just Glue/tape a bit of radioactive power into the scratch. Launch 200 at any shipping – mostly to contaminate the vessel, the oil, and disrupt the global shipping insurance market, his ship assets are financed/leveraged etc And at the oil terminals (and at anything if economic value really, i think it said).
The idea, as explained, Was to do low level contaminating – not explode stuff really.
More tyrion greek wild fire, less danny with all her dragons and death
— well, now analyzing that bit of tv fantasy induced dreamland —
Patriot missiles are useless.m (or helpful). F-15s are useless against one man walking a rucksack of rockets. Warthogs useless if he is walking alone or through (eg bombed out rubble Cities a la stalingrad) . Viet Cong proved that (as did russia itself, facing unlimited nazi resources, for a while)
All the us can do is commit ground forces (which will make trump mad as hell and cost him his glorious ceasar like triumph). Or make iraq play the role (hint).
Draw them in, make it another long drawn out iraq (where the us military strategy suffered from inability to deal with the asymmetry lying behind every drain and culvert, and left a million soldiers with long term costs of ptsd , from the constant stress of having no ice cream from the px for dinner and, ugh, trumps profile on their service medal!
As you saw in iraq, the us army is bad at holding territory. Its technology and training is counterproductive to that kind of fight.
Now you really are fighting asymmetrically. Its Iraq all over again, as they would have to attempt to contain the tiny missile threat with the wrong wrong weapon system designed mostly for tv victories, tv triumphs, etc. saddam got that bit right!
Oh and put containers of spent fuel on all rooftops, so when they start bombing they know they spread the radioactivity into the planet’s air supply. Now the neighbor countries will care … about the bombing campaign (since they get real consequences, within the 24h news cycle, as planetary air moves fast!)
What do you do with your icbms? Use them or lose them, day 1 , first hour, second minute after the first radar blip. Just change out the silly explosive warhead for spent fuel. Let the patriot hit it mid flight and setup self destruct …so it spreads the fuel way up high in the atmosphere… ready for the next rains…
Lets see how the us military strategy handles it, now there is a fifty year global consequences, with unknown spread of the war zone
Remember vircingetrix (sp?) the celt is just as famous as Julius Caesar, a few thousand years later. You can win against an empire by losing.
Venezuela court to hold bbc in contempt?
Court “claimed”
That is offensive biased (propagandized) reporting
If the bbc knows its reporting is available in vz, I’d hold the institution in contempt of the court’s authority –
Notwithstanding that they are bunch of maduro cronies…
They are still the one and only constitutional court of vz.
Uk Ecuador assange and bail
Presumably snarky uk magistrates will be applauding these moves by court fugitives
Sir magistrate?
Your honour?
Book deal?
Uk corruption – the honours system.
Its how politics is injected into court processes, though. Not everything is legal or equity.
Sometimes its just regal pomposity, with full face contradictions
Foxnews and trump: the stupid and the smart

Trump has one hitler like quality: he can get people to act like stupid sheep and follow him into the field of doodoo; willingly, obediently, unthinkingly.
Fox news reader folks are very American – entirely able to embrace the contradiction that they broke the deal (that we haven’t made yet)
And that is American exceptionalism, defined. Don’t you see the logic in embracing the contradiction?
I call trump a clown, but thats not to say, like hitler, he isn’t a “smart” clown when it comes to the process of maca : make america clown again
In english we call it cheating. In america, cheating is just of several important exceptional class skills you must learn (to get rich).
You have have to think how the Americans strangely ended up with all the land in California…after statehood (largely through american cheating and sciestering , a central social skill)
Main focus of uk spying is….
Come on! Didnt you learn your history?
Recall eliz 1 most famous spymaster!
The first target of uk spying is, was, and always will be uk folk!!
Thus is more fun than the wikileaks story about spying on the internet; and brexit combined!!


You must be logged in to post a comment.